- ... Page1
- aka so_penible_animation
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... m\'emoire2
- le coût de calcul est est la
moitié du coût de calcul de la FFT !
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polyphase3
- le terme
polyphase vient de la théorie du filtrage numérique où il est
utilisé pour décrire le partitionement d'une séquence
déchantillons en plusieurs sous-séquences qui peuvent être
traitées en parallèle, les sous-séquences peuvent-Ítre vues
comme des versions d'elle-même décalées en phase d'où le
nom.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...odd)4
- moyen mnémotechnique :
even a un nombre de lettres pair, odd a
un nombre de lettres impair
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
 5
5
- l'inversion
temporelle (
 ) est nécessaire pour compenser le délai
introduit par le filtrage
) est nécessaire pour compenser le délai
introduit par le filtrage
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Laurent6
- Soit la
transformée en Z d'un filtre FIR :
![$h(z)=\sum\limits_{k=p}^q
h[k]z^{-k}$](img53.png) Cette somme est aussi nommée polynôme de Laurent ou
encore série de Laurent.
Cette somme est aussi nommée polynôme de Laurent ou
encore série de Laurent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... reste7
- Pour réaliser la division avec reste on utilise l'algorithme d'Euclide.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... d'Euclide8
- Exemple : soit
 On applique l'algorithme d'Euclide :
On applique l'algorithme d'Euclide :
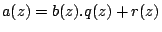 .
Soient ici
.
Soient ici
 et
et

 signifie modulo. La procédure est itérative, plusieurs choix sont en général
possible pour le choix de l'ordre du diviseur.
signifie modulo. La procédure est itérative, plusieurs choix sont en général
possible pour le choix de l'ordre du diviseur.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... dividende9
- le nombre
de possibilités différentes est lié aux degrés (noté
 ) des
polynômes de Laurent des diviseurs et dividendes. Le degré d'un
polynôme de Laurent quelconque
) des
polynômes de Laurent des diviseurs et dividendes. Le degré d'un
polynôme de Laurent quelconque  défini par
défini par
![$h(z)=\sum\limits_{k=p}^q
h[k]z^{-k}$](img53.png) est
est  . Soit
. Soit  , si
le degré du diviseur et du dividende sont égaux
alors le nombre de possibilités est
, si
le degré du diviseur et du dividende sont égaux
alors le nombre de possibilités est  , si
maintenant
, si
maintenant  alors le nombre de possibilités est
alors le nombre de possibilités est 
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
![$h(z)=\sum\limits_{k=p}^q
h[k]z^{-k}$](img53.png) Cette somme est aussi nommée polynôme de Laurent ou
encore série de Laurent.
Cette somme est aussi nommée polynôme de Laurent ou
encore série de Laurent.
![]() signifie modulo. La procédure est itérative, plusieurs choix sont en général
possible pour le choix de l'ordre du diviseur.
signifie modulo. La procédure est itérative, plusieurs choix sont en général
possible pour le choix de l'ordre du diviseur.
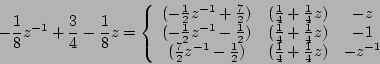
![$h(z)=\sum\limits_{k=p}^q
h[k]z^{-k}$](img53.png) est
est