Daubechies(4) signifie que les filtres de cette ondelette possèdent
4 coefficients et ![]() moments
nuls.
moments
nuls.
On a aussi :
et
On trouve son expression dans les tables ou dans [Daubechies] :
![\begin{displaymath}
\begin{array}{ccc}
h_0 = h[0] &=& \frac{1+\sqrt{3}}{4\sqrt{...
...}}\\
h_3 = h[3] &=& \frac{1-\sqrt{3}}{4\sqrt{2}}
\end{array}\end{displaymath}](img119.png)
On a les propriétés intéressantes suivantes :
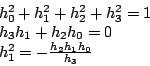
soient
![\begin{displaymath}
\begin{array}{ccc}
h[0]&=&.482962913145\\
h[1]&=&.836516303738\\
h[2]&=&.224143868042\\
h[3]&=&-.129409522551
\end{array}\end{displaymath}](img121.png)
et
d'où
et
de la même façon pour ![]()
et
d'où
On va écrire une étape de lifting primaire :
Alors,
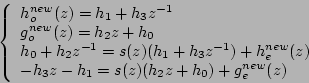
On utilise alors la division euclidienne : (on note que plusieurs factorisations sont possibles suivant l'ordre dans lequel on choisit de prendre en compte diviseur et dividende 9.)
Par exemple :
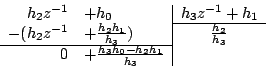
ou alors
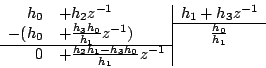
etc. ...
On se limite à l'exploration de la première solution (les autres aboutiront aussi à des formulations différentes mais équivalentes).
On a alors :
et
on explicite alors ![]() :
:
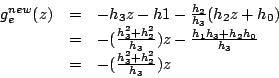
d'où
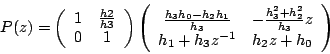
Maintenant, le lifiting dual :
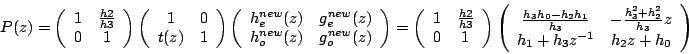
alors,

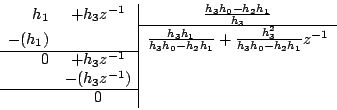
donc
alors,
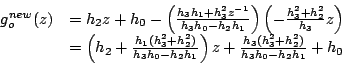
Or
d'où
Voilà :

On peut maintenant mettre en évidence la mise à l'échelle
d'abord en réécrivant un peu les derniers coefficients obtenus à
l'aide des formules sur les coefficients ![]() (
(![]() ) :
) :
d'où
et
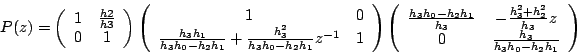
On a aussi
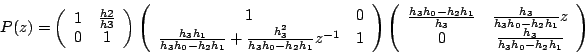
On peut donc introduire l'étape de mise à l'échelle (normalisation), en remarquant que
d'où finalement
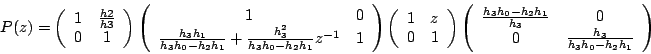
c'est-à-dire
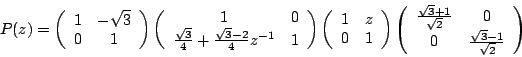
et alors :
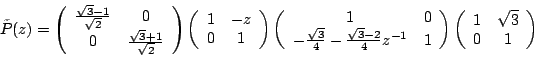
On peut de façon plus condensée (que l'écriture matricielle) écrire le pseudo code pour
l'algorithme de calcul in place, ![]() et
et ![]() représente
les coefficients pairs et impairs du signal (respectivement),
représente
les coefficients pairs et impairs du signal (respectivement), ![]() représente les détails (i.e. les coefficients issu du filtrage
passe haut, donc les coefficients d'ondelettes),
représente les détails (i.e. les coefficients issu du filtrage
passe haut, donc les coefficients d'ondelettes), ![]() représente le
signal grossier (smooth) issu du fitlrage passe-bas et donc les
coefficients d'échelle.
représente le
signal grossier (smooth) issu du fitlrage passe-bas et donc les
coefficients d'échelle.

Pour le passage à une résolution supérieure on prend le code
précédent que l'on réinitialise en commençant par :