Transformée en ondelettes version lifting

La transformation en ondelettes version lifting est un processus permettant entre autres d'optimiser le nombre d'opérations à exécuter et l'occupation mémoire².

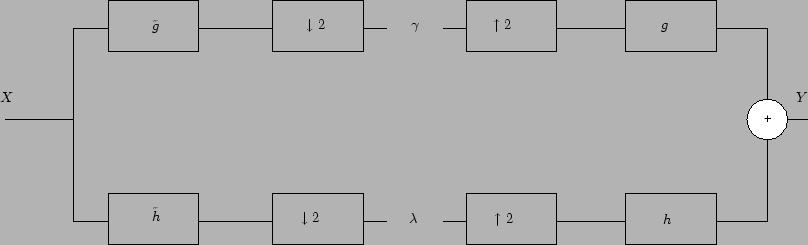
Le processus le plus courant pour obtenir une transformation en ondelettes est d'utiliser un banc de filtres (cf. Figure 1), cependant lorsqu'on regarde cette façon de procéder on constate que l'on effectue un sous-échantillonnage par deux après une opération de filtrage : on a donc dépenser en pure perte la moitié du coût de calcul effectué par le filtrage.

L'opération de Lifting en ondelettes peut-être vu comme la transformation réalisée par le banc de filtres, mais en intervertissant les phases de filtrage et de sous-échantillonnage. On limite ainsi le nombre d'opérations a effectuer mais, nous perdons en revanche la propriété d'invariance par translation.

Une autre propriété intéressante est que le schéma de lifting est facilement inversible.

Le schéma de lifting est aussi lié au processus d'interpolation (non explicitement étudié ici).

On désigne par $\gamma$ les coefficients d'ondelettes et par $\lambda$ les coefficients d'échelle.

Pour une ondelette particulière (i.e. un couple de filtres ($h$,$g$,$\tilde{h}$, $\tilde{g}$ pour l'implémentation par banc de filtres), caractérisé en outre par disons $n$ moments nuls (jouant un rôle dans le processus de décroissance des coefficients d'ondelettes à travers les résolutions) pour le filtre primaire et $\tilde{n}$ moments nuls pour le filtre dual, le schéma d'implantation par lifting permet d'obtenir facilement des ondelettes de moments $n$ et $\tilde{n}$ plus élevé. On a donc lifté (i.e.élevé) l'ordre de cette ondelette par ce schéma (d'où la justification du nom lifting).

Figure 1: Schéma d'une implémentation en banc de filtres d'une transformation en ondelettes : le signal original $X$ passe par les deux filtres complémentaires $\tilde{h}$ (passe-bas) et $\tilde{g}$ (passe-haut) en sortie on peut sous-échantillonner par 2 ($\downarrow2$), on obtient alors respectivement des coefficients d'ondelettes $\gamma$ et des coefficients d'échelle $\lambda$. La reconstruction du signal s'effectue par sur-échantillonnage par insertion de zéros ($\uparrow2$) et passage par les filtres de synthèse $h$ et $g$ puis par addition pour obtenir le signal $Y$.

On utilise : les ondelettes paresseuses (lazy wavelets) qui servent à séparer un vecteur en composantes paires et impaires, ainsi qu'une matrice polyphase qui permet de travailler sélectivement sur les composantes paires ou impaires du signal. On va factoriser la matrice polyphase et introduire alors deux opérations : une opération de prédiction (Predict) qui prédit les échantillons de rang pair à partir des échantillons de rang impair; une opération de mise-à-jour (Update) qui permet de conserver sur une partie du signal la valeur moyenne de l'ensemble du signal.

Le formalisme utilisé est celui des articles de références [Sweldens, Valens]. (Attention cependant aux écarts de notations entre les différents articles).

Cette transformation va en outre permettre de réaliser une transformation sur des entiers qui donne des entiers. Cependant il faudra utiliser une étape supplémentaire utilisant le lifting pour la mise à l'échelle.