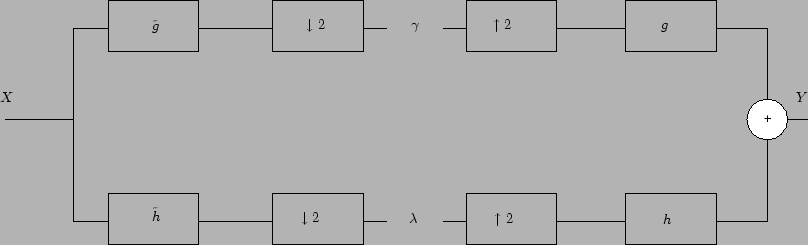
On part des filtres d'analyse et de reconstruction de l'analyse multi-résolution classique par banc de filtres suivant le schéma classique de la Figure 1 :
|
|
|
|
|
|
|
|
Attention aux notations, dans certaines références, on
trouve souvent
![]() et
et
![]() . Dans les
expressions des filtres, le coefficient souligné correspond à
l'indice
. Dans les
expressions des filtres, le coefficient souligné correspond à
l'indice ![]() .
.
Les filtres doivent en outre satisfaire les formules suivantes :
On a besoin de construire la matrice polyphase3 ![]() (ainsi que sa matrice duale
(ainsi que sa matrice duale ![]() ), on utilise la
formule suivante de décomposition polyphase sur les filtres précédents :
), on utilise la
formule suivante de décomposition polyphase sur les filtres précédents :
| (1) |
Il vient assez facilement :
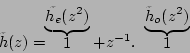
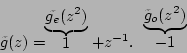
sachant que det![]() et que pour det
et que pour det![]() on a les
propriétés suivantes :
on a les
propriétés suivantes :
![]()
![]()
![]()
![]()
Ces proporiétés montrent que pour passer de l'analyse à la
synthèse (de ![]() à
à ![]() ) il suffit si det
) il suffit si det![]() , de
prendre la matrice des cofacteurs en
changeant de signe.
, de
prendre la matrice des cofacteurs en
changeant de signe.
de plus sachant que
![]() 5
5
 |