La démarche ici est en quelque sorte la démarche inverse afin de pouvoir passer de forme
connue de pairs de filtres d'ondelettes à leur implémentation en terme de
lifting d'ondelettes.
on peut réécrire
En itérant cet exemple, on peut arriver à obtenir une matrice polyphase qui
est de la forme :
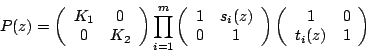
où ![]() et
et ![]() sont deux constantes (différentes de zéro) que
l'on peut éventuellement factoriser en quatre étapes de lifting.
sont deux constantes (différentes de zéro) que
l'on peut éventuellement factoriser en quatre étapes de lifting.